Złamanie klucza krzywej eliptycznej 5-bitowej za pomocą 133-kubitowego komputera kwantowego ⚛️ Eksperyment ten łamie 5-bitowy klucz kryptograficzny krzywej eliptycznej przy użyciu algorytmu Shora. Wykonany na 133-kubitowym ibm_torino od @IBM z użyciem @qiskit, 15-kubitowy obwód, składający się z 10 logicznych kubitów i 5 ancilli, interferuje w ℤ₃₂, aby wydobyć tajny skalar k z relacji klucza publicznego Q = kP, nigdy nie kodując k bezpośrednio w oraklu. Z 16 384 prób, kwantowa interferencja ujawnia diagonalny grzbiet w przestrzeni wyników QFT 32x32. Kwantowy obwód, mający ponad 67 000 warstw, wyprodukował ważne wzory interferencyjne pomimo ekstremalnej głębokości obwodu, a klasyczne przetwarzanie po pomiarze ujawniło k = 7 w 100 najlepszych odwracalnych wynikach (a, b). Przegląd kodu 1. Kodowanie grupowe Ogranicz uwagę do podgrupy rzędu 32 ⟨𝑃⟩ krzywej eliptycznej nad 𝐹_p. Mapuj punkty na liczby całkowite: 0𝑃 -> 0,  1𝑃 -> 1, …, 31𝑃 -> 31. Prawo grupy staje się dodawaniem modularnym: (𝑥𝑃) + (𝑦𝑃) = ((𝑥 + 𝑦) mod 32))𝑃. Eksperyment ten wykorzystuje krzywą eliptyczną nad F_p​ z cykliczną podgrupą rzędu 32, mapując P -> 1 i Q = 7P -> 23 w ℤ₃₂​. Kod zakłada wstępnie obliczoną mnożenie skalarne, abstrahując od jawnych współrzędnych. 2. Rejestry kwantowe Rejestr a: pięć kubitów dla wykładnika 𝑎 ∈ {0, …, 31}. Rejestr b: pięć kubitów dla 𝑏 ∈ {0, …, 31}. Rejestr p: pięć kubitów zainicjowanych do ∣0⟩, aby przechować indeks punktu. Klasyczny rejestr c: 10-bitowy rejestr do rejestrowania zmierzonych wartości a i b. 3. Przygotowanie superpozycji Zastosuj bramki Hadamarda do każdego kubitu w a i b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Budowa orakla U_f Celem jest odwracalna mapa: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Dodaj aP: dla każdego bitu a_i (waga 2^𝑖), dodaj (2^𝑖 P) mod 32 Dodaj bQ: oblicz (2^𝑖 𝑄) mod 32, a następnie dodaj kontrolowane na 𝑏_𝑖. Te operacje wykorzystują 5-kubitowe bramki permutacyjne kontrolowane. Wszystkie stałe pochodzą od generatora krzywej eliptycznej P i punktu publicznego Q. Żadna bramka nigdy nie odnosi się bezpośrednio do tajnego k. 5. Globalny stan po oraklu Stan ewoluuje do: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, gdzie f(a, b) = a + kb (mod32). a, b 6. Izolacja rejestru punktów Algorytm potrzebuje tylko relacji fazowej w 𝑎, 𝑏. Bariera izoluje p. 7. Kwantowa transformacja Fouriera (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Wzór interferencyjny Wspólna amplituda dla obserwacji (u, v) to: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), co tworzy diagonalny grzbiet w siatce wyników 32x32. 9. Pomiar Zmierz wszystkie dziesięć logicznych kubitów. Wyniki koncentrują się na 32 odrębnych parach spełniających u + kv ≡ 0 (mod 32). 10. Klasyczne przetwarzanie po pomiarze Ciągi bitowe są odwracane i analizowane w pary (a, b). Zachowaj tylko wiersze, w których gcd⁡(b, 32) = 1, zapewniając, że b jest odwracalne. Kandydat na klucz oblicza się jako: k = (-a) b^(-1) mod 32 Skrypt następnie: Wydobywa 100 najwyżej liczących się odwracalnych wyników (a, b). Oblicza k dla każdego. Drukuje każdą parę (a, b), odzyskane k i liczbę. Ogłasza sukces, jeśli k = 7 pojawia się w 100 najlepszych. 11. Weryfikacja i przechowywanie Poprawny skalar k = 7 jest potwierdzany, jeśli pojawia się w 100 najlepszych odwracalnych wynikach. Wszystkie surowe liczniki bitowe, układ kubitów i metadane są zapisywane w formacie JSON do dalszej wizualizacji i analizy. Wyniki 2025-06-25 19:41:29,294 | INFO | Głębokość obwodu 67428, liczba bramek OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Przesyłanie zadania z opcjami {'options': {}, 'version': 2, 'support_qiskit': True} SUKCES — k = 7 znaleziono w 100 najlepszych wynikach 100 najlepszych odwracalnych par (a, b) i odzyskane k: (a= 8, b=11) → k = 8 (liczba = 63) (a=12, b= 9) → k = 20 (liczba = 58) (a= 0, b= 3) → k = 0 (liczba = 54) (a= 1, b= 9) → k = 7 (liczba = 54) <<< (a=28, b= 1) → k = 4 (liczba = 53) (a= 0, b=11) → k = 0 (liczba = 53) (a= 8, b= 9) → k = 24 (liczba = 53) (a= 8, b= 3) → k = 8 (liczba = 53) ... (a=11, b= 3) → k = 7 (liczba = 41) <<< ... (a=25, b= 1) → k = 7 (liczba = 32) <<< To uruchomienie skutecznie odzyskało tajny skalar k = 7 przy użyciu 5-bitowego klucza ECC (podgrupa rzędu 32), rozszerzając mój wcześniejszy atak 4-bitowy do przestrzeni z 1024 możliwymi kombinacjami (a, b) i φ(32) = 16 odwracalnymi wartościami b. k = 7 pojawia się trzy razy w 100 najlepszych: (a = 1, b = 9) -> k = 7 z 54 liczbami (a = 11, b = 3) -> k = 7 z 41 liczbami (a =25, b = 1) -> k = 7 z 32 liczbami To są stany o wysokiej częstotliwości, co czyni je wiarygodnymi wektorami ataku w ramach klasycznego przetwarzania po pomiarze. Liczby wykazują koncentrację wokół strukturalnych relacji modularnych: a + kb ≡ 0 mod 32. Pojawiają się one jako diagonalne grzbiety w przestrzeni pomiarowej 32x32. Kilka wartości k powtarza się często (k = 0, 24, 28), co pokazuje probabilistyczne nakładanie się wewnętrzne do kwantowej interferencji, niektóre z nich to fałszywe pozytywy z szumów lub aliasingu z innymi równaniami modularnymi. Głębokość obwodu wynosiła 67 428, z łączną liczbą 106 455 bramek, co odzwierciedla dużą, złożoną rutynę kwantową dla kontrolowanej arytmetyki indeksów modularnych. To może być największa liczba bramek, jaką użyłem w obwodzie. Liczby bramek dla obwodu: sx: 56613 cz: 34319 rz: 15355 x: 157 measure: 10 barrier: 1 Łączna liczba bramek: 106455 Głębokość: 67428 Szerokość: 133 kubity | 10 clbits Eksperyment ten trwał 54 sekundy na 'ibm_torino'. Profil szumów jest nien jednorodny, ale malejący, co oznacza, że system kwantowy prawdopodobnie rozwiązał dominujące harmoniczne w interferencji, ale rozmył drobniejsze struktury. Ogon rozkładu nadal zawiera ważne kandydaty k = 7, co wspiera ataki kwantowe w stylu słownikowym, gdzie skany wyników top-N (N = 100) są wystarczające do odzyskania klucza. 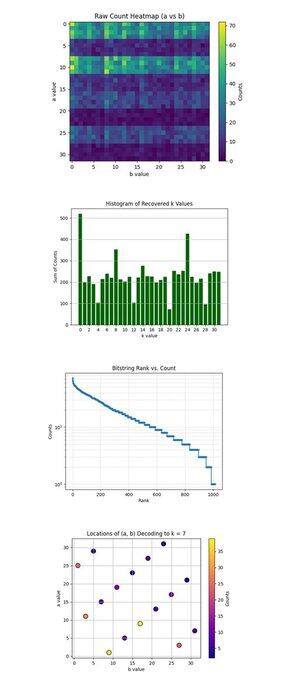Mapa cieplna surowych liczników (a vs b) powyżej (pełny kod na Qwork) pokazuje siatkę 32x32, która reprezentuje obserwowane liczby dla każdej pary (a, b) po uruchomieniu obwodu Shora. Mapa cieplna pokazuje pasmową i nierówną dystrybucję, wskazując na grzbiety interferencyjne, a nie szum. Niektóre wiersze (wartości a) mają widocznie wyższą koncentrację, co sugeruje konstruktywną interferencję wzdłuż konkretnych rozwiązań a + kb ≡ 0 mod 32. Histogram odzyskanych wartości k powyżej (pełny kod na Qwork) agreguje całkowite liczby dla każdego odzyskanego klucza skalarnego k ∈ Z₃₂, uzyskanego za pomocą k = −ab^(−1) mod 32. Ogromny szczyt przy k = 0 i kolejny wokół k = 24 są dominujące. Poprawny klucz k = 7 nie jest najwyższy, ale jest dobrze reprezentowany (~54 + 41 + 32 = 127 liczb w różnych parach (a, b)). To pokazuje, że hakerzy mogą zaatakować słownikowo większą ilość wyników. Wykres rangi ciągu bitowego w porównaniu do liczby (skala logarytmiczna) powyżej (pełny kod na Qwork) pokazuje wykres rangi podobny do Zipfa wszystkich ciągów bitowych według malejącej liczby. Oś y w skali logarytmicznej pokazuje wykładniczy ogon, większość wyników występuje <10 razy. Głowa (około 50) ciągów bitowych ma znacznie wyższą prawdopodobieństwo, co wskazuje na szczyty konstruktywnej interferencji. Można zbudować kwantowy heurystyczny atak słownikowy, który zbiera tylko najlepsze N ciągi bitowe z wykładniczym zwrotem sygnału. To potwierdza, że struktura sygnału do szumu kwantowego pozostaje nienaruszona, nawet przy dłuższych obwodach (67428 głębokości). Lokalizacje (a, b) dekodujące do k = 7 powyżej (pełny kod na Qwork) pokazują, że każdy punkt to para (a, b), która dekodowała do k = 7. Intensywność koloru odpowiada liczbie wystąpień tej pary. Wykres pokazuje stosunkowo jednolitą dystrybucję w (a, b), ale z lokalnymi szczytami przy (1, 9), (11, 3), (25, 1). Wiele kombinacji (a, b) zbiega się do k = 7 z nien jednorodną wielokrotnością. Z punktu widzenia kryptanalizy, to potwierdza, że algorytm Shora może niezawodnie łamać klucze ECC, nawet gdy poprawne k nie jest najlepszym wynikiem. 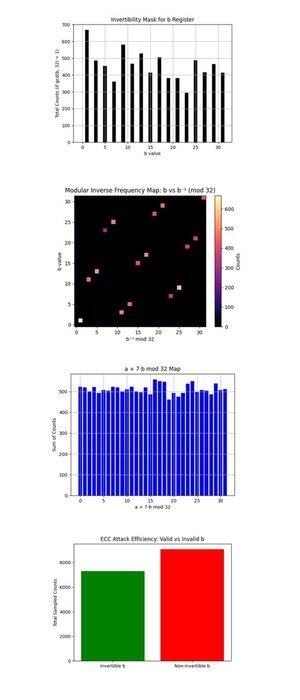Maska odwracalności dla rejestru b powyżej (pełny kod na Qwork) pokazuje wykres słupkowy liczby dla każdego b ∈ {0, …, 31}, które są względnie pierwsze z 32 (gcd⁡(b, 32) = 1, tylko te są odwracalne modulo 32 i użyteczne do odzyskiwania k za pomocą: k = (−a)b^(−1) mod 32. Odwracalne b są dobrze zaludnione, co pokazuje, że obwód rzeczywiście wyprodukował możliwe do odzyskania kandydaty. Większa jednorodność tutaj zwiększyłaby moc przetwarzania po pomiarze, idealnie, powinny być płaskie. Mapa częstotliwości odwrotności modularnej: b vs b^(−1) mod 32 powyżej (pełny kod na Qwork) pokazuje mapę cieplną, jak często każde odwracalne b mapuje się na odpowiadające mu odwrotne modularne b^(−1) mod 32, ważone przez liczby wyników. Większość punktów znajduje się na czystej bijektywnej linii, każde b mapuje się czysto na unikalne b^(−1), potwierdzając poprawność odwrotności modularnej. Jaśniejsze obszary (w pobliżu lewego dolnego lub prawego górnego rogu) pokazują preferowane b z próbkowania kwantowego. Brak szumów poza przekątną lub klasteryzacji, dobry znak czystej struktury modularnej. Mapa a + 7b mod 32 powyżej (pełny kod na Qwork) zakłada k = 7 i rysuje wartość (a + 7b) mod 32 we wszystkich wynikach. Dystrybucja jest prawie jednorodna. To sugeruje brak ostrego grzbietu interferencyjnego, jak w przypadku 4-bitowym. Dlaczego? Obwód 5-bitowy (z 10 logicznymi kubitami) rozkłada amplitudę cieńsze w 1024 wynikach, zmniejszając kontrast. Mimo to poprawny klucz był nadal możliwy do odzyskania, co wskazuje na wiele słabo konstruktywnych ścieżek, a nie kilka dominujących. Efektywność ataku ECC: Ważne vs Nieważne b powyżej (pełny kod na Qwork) pokazuje całkowite liczby z próbek z odwracalnym b (użytecznym do odzyskiwania klucza) w porównaniu do nieodwracalnego b (bezużytecznego). Ponad połowa wyników jest marnowana na nieważne wartości b (gcd⁡(b, 32) != 1). Następny projekt na złamanie 6-bitowe mógłby wykorzystać maskowanie orakla lub filtrowanie po wybraniu na ważnych domenach b. 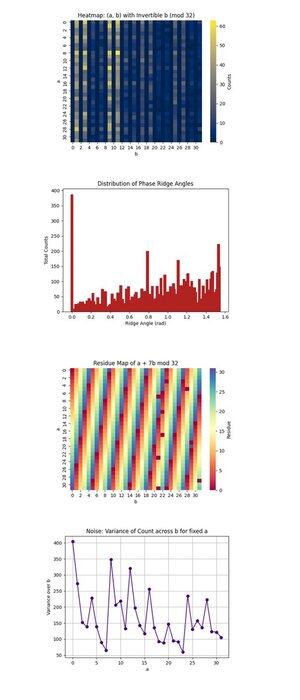Mapa cieplna: (a, b) z odwracalnym b (mod 32) powyżej (pełny kod na Qwork) koncentruje się tylko na parach (a, b), gdzie b jest odwracalne modulo 32, co jest niezbędnym warunkiem do odzyskania k. Pokazuje, gdzie kwantowa interferencja koncentruje się w przestrzeni 1024 punktów. Obszary o wysokiej intensywności ujawniają preferowane ścieżki interferencyjne, sugerując, że stan kwantowy ewoluował nien jednorodnie, prawdopodobnie faworyzując pewne orbity pod mnożeniem modularnym. Potwierdza to wystarczającą koherencję sygnału w niektórych obszarach, aby izolować ważne kandydaty. Rozkład kątów grzbietów fazowych powyżej (pełny kod na Qwork) grupuje kąty utworzone przez wektory (-a, b) w płaszczyźnie, modulo π, które w przybliżeniu odpowiadają grzbietom fazowym w przestrzeni QFT. Szczyty w histogramie wskazują na silne wyrównania, rezonanse, w formie u + kv ≡ 0, co oznacza, że obwód skutecznie zakodował k w wzorze interferencyjnym, mimo że pełna przestrzeń stanów jest ogromna. Wiele dominujących kątów sugeruje, że obecne są harmoniczne ukrytego przesunięcia. Mapa resztowa a + 7b mod 32 powyżej (pełny kod na Qwork) wizualizuje resztę wyjściową dla konkretnego klucza docelowego k = 7, w całej przestrzeni (a, b). Jakiekolwiek spójne pasma lub symetrie tutaj wskazują, jak dobrze interferencja wzmocniła ważne rozwiązania (gdzie ta wartość równa się 0). Można zaobserwować, które obszary 1024 siatki odpowiadają a + 7b ≡ 0, potwierdzając, że struktura orakla doprowadziła do udanego odcisku klucza. Szum: Wariancja liczby wzdłuż b dla stałego a powyżej (pełny kod na Qwork) pokazuje, jak hałaśliwe lub stabilne były wyjściowe liczby dla każdego stałego a, gdy zmieniamy b. Wysoka wariancja oznacza, że niektóre wartości b prowadzą do silnego wzmocnienia, podczas gdy inne nie, co sugeruje wrażliwość obwodu lub szum na zapleczu dla tego wiersza a. Gładkie obszary sugerują koherencję kwantową, podczas gdy szczyty mogą wskazywać na dekoherencję lub propagację błędów podczas oceny orakla. Na koniec, ten eksperyment skutecznie złamał 5-bitowy klucz krzywej eliptycznej przy użyciu algorytmu Shora wykonanego na 133-kubitowym procesorze kwantowym IBM, rozszerzając wcześniejszy wynik 4-bitowy do znacznie większej przestrzeni interferencyjnej (32x32 = 1024 wyniki). Ten obwód zakodował orakl w ℤ₃₂, nigdy nie odnosząc się do tajnego skalaru k, i wykorzystał arytmetykę grupy modularnej, aby splątać skalar w interferencji fazowej. Kwantowy obwód, mający ponad 67 000 warstw, wyprodukował ważne wzory interferencyjne pomimo ekstremalnej głębokości obwodu, a klasyczne przetwarzanie po pomiarze ujawniło k = 7 w 100 najlepszych odwracalnych wynikach (a, b). Dzięki wizualizacjom ten eksperyment potwierdził struktury diagonalnych grzbietów, maski odwracalności i harmoniczne wyrównanie grzbietów interferencyjnych, potwierdzając, że koherencja kwantowa pozostała wystarczająco silna, aby wzmocnić poprawną relację modularną. To ustanawia, że algorytm Shora nadal skaluje się w ramach głębszych reżimów obwodowych i że strategie odzyskiwania kluczy oparte na słownikach (enumeracja 100 najlepszych) pozostają wykonalne w miarę wzrostu długości bitów, pokazując wyraźną przewagę kwantową nawet w hałaśliwych warunkach rzeczywistych. Kod # Główny obwód # Importy import logging, json from math import gcd import numpy as np from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile from qiskit.circuit.library import UnitaryGate, QFT from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2 import pandas as pd # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTANCE = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" SHOTS = 16384 # Parametry krzywej zabawowej (podgrupa rzędu 32 E(F_p)) ORDER = 32 # |E(F_p)| = 32 P_IDX = 1 # Generator P -> indeks 1 Q_IDX = 23 # Punkt publiczny Q = kP, tutaj „23 mod 32” dla k = 7 # Pomocnik logowania logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(levelname)s | %(message)s") log = logging.getLogger(__name__) # Wybór kubitów na podstawie kalibracji def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.columns = df.columns.str.strip() winners = ( df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"], ascending=[True, False, False]) ["Qubit"].head(n).tolist() ) log .info("Najlepsze fizyczne kubity: %s", winners) return winners N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, punkt PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL) # Stały dodawacz modulo 32 jako użyteczna bramka def add_const_mod32_gate(c: int) -> UnitaryGate: """Zwróć bramkę 5-kubitową, która mapuje |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.zeros((32, 32)) for x in range(32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant): """Zastosuj |x⟩ → |x+constant (mod 32)⟩ kontrolowane przez jeden kubit.""" qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg]) # Orakl U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (arytmetyka indeksu mod 32) def ecdlp_oracle(qc, a_reg, b_reg, point_reg): for i in range(N_Q): constant = (P_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, a_reg[i], point_reg, constant) for i in range(N_Q): constant = (Q_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, b_reg[i], point_reg, constant) # Buduj pełny obwód Shora def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.barrier() qc.append(QFT(N_Q, do_swaps=False), a) qc.append(QFT(N_Q, do_swaps=False), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) return qc # Wykonanie IBM Runtime service = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, instance=INSTANCE) backend = service.backend(BACKEND) log .info("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend=backend, initial_layout=PHYSICAL, optimization_level=3) log .info("Głębokość obwodu %d, liczba bramek %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(mode=backend) job = sampler .run([trans], shots=SHOTS) result = job.result() # Klasyczne przetwarzanie po pomiarze creg_name = trans.cregs[0].name counts_raw = result[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): return int(bs[::-1], 2) counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v for k, v in counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Kryteria sukcesu. Sprawdź 100 najlepszych odwracalnych wierszy dla k = 7 top_invertibles = [] for (a_val, b_val), freq in top: if gcd(b_val, ORDER) != 1: continue inv_b = pow(b_val, -1, ORDER) k_candidate = (-a_val * inv_b) % ORDER top_invertibles.append(((a_val, b_val), k_candidate, freq)) if len(top_invertibles) == 100: break # Sprawdź sukces i wydrukuj wyniki found_k7 = any(k == 7 for (_, k, _) in top_invertibles) if found_k7: print("\nSUKCES — k = 7 znaleziono w 100 najlepszych wynikach\n") else: print("\nOSTRZEŻENIE — k = 7 NIE znaleziono w 100 najlepszych wynikach\n") print("100 najlepszych odwracalnych par (a, b) i odzyskane k:") for (a, b), k, count in top_invertibles: tag = " <<<" if k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (liczba = {count}){tag}") # Zapisz surowe dane out = { "eksperyment": "ECDLP_32pts_Shors", "backend": backend .name, "fizyczne_kubity": PHYSICAL, "strzały": SHOTS, "liczby": counts_raw } JSON_PATH = "/Users/steventippeconnic/Documents/QC/Shors_ECC_5_Bit_Key_0.json" with open(JSON_PATH, "w") as fp: json.dump(out, fp, indent=4) log .info("Wyniki zapisane → %s", JSON_PATH) # Koniec Pełny kod dla wszystkich wizualizacji z użyciem danych z uruchomienia na Qwork.