كسر مفتاح منحنى بيضاوي الشكل 5 بت باستخدام كمبيوتر ⚛️ كمي 133 كيوبت تكسر هذه التجربة مفتاح تشفير منحنى بيضاوي الشكل 5 بت باستخدام خوارزمية شور. تم تنفيذه على ibm_torino 133 كيوبت من @IBM مع @qiskit ، وهي دائرة من 15 كيوبت ، تتكون من 10 كيوبت منطقي و 5 أنسيلا ، تتداخل على Z₃₂ لاستخراج العددي السري k من علاقة المفتاح العام Q = kP ، دون ترميز k مباشرة في أوراكل. من 16,384 طلقة ، يكشف التداخل الكمي عن سلسلة من التلال القطرية في مساحة نتائج 32 × 32 QFT. أنتجت الدائرة الكمومية ، التي يزيد عمقها عن 67,000 طبقة ، أنماط تداخل صالحة على الرغم من عمق الدائرة الشديد ، وكشفت المعالجة اللاحقة الكلاسيكية k = 7 في أفضل 100 نتيجة قابلة للعكس (أ ، ب). تجول التعليمات البرمجية 1. ترميز المجموعة قم بتقييد الانتباه إلى المجموعة الفرعية من الترتيب 32 ⟨P⟩ لمنحنى بيضاوي الشكل على F_p. تشير الخريطة إلى الأعداد الصحيحة: 0P -> 0 ، 1P -> 1 ، ... ، 31P -> 31. يصبح قانون المجموعة إضافة معيارية: (xP) + (yP) = ((x + y) mod 32)) P. تستخدم هذه التجربة منحنى بيضاوي الشكل على F_p مع مجموعة فرعية دورية من الترتيب 32 ، ورسم خرائط P -> 1 و Q = 7P -> 23 في Z₃₂. يفترض الكود الضرب العددي المحسوب مسبقا ، مما يؤدي إلى تجريد الإحداثيات الصريحة. 2. السجلات الكمومية سجل أ: خمسة كيوبتات للأس أ ∈ {0 ، ... ، 31}. سجل ب: خمسة كيوبتات ل b ∈ {0 ، ... ، 31}. سجل p: تمت تهيئة خمسة كيوبتات إلى ∣0⟩ للاحتفاظ بمؤشر النقاط. السجل الكلاسيكي c: سجل 10 بتات لتسجيل القيم المقاسة ل a و b. 3. إعداد التراكب ضع Hadamards على كل كيوبت في أ و ب: 31 1/32 ∑ ∣أ⟩_a ∣ ب ⟩_b ∣0⟩_p أ ، ب = 0 4. U_f بناء أوراكل الهدف هو خريطة قابلة للعكس: ∣ أ⟩ ∣ ب ⟩ ∣ 0⟩ -> ∣ أ ⟩ ∣ ب ⟩ ∣ aP + bQ ⟩. أضف aP: لكل بت a_i (الوزن 2 ^ i) ، أضف (2 ^ i P) mod 32 أضف bQ: احسب (2 ^ i Q) mod 32 ، ثم أضف التحكم في b_i. تستخدم هذه بوابات التقليب التي يتم التحكم فيها 5 كيوبت. جميع الثوابت مشتقة من مولد المنحنى الإهليلجي P والنقطة العامة Q. لا توجد بوابة تشير مباشرة إلى السر k. 5. الحالة العالمية بعد أوراكل تتطور الدولة إلى: 1/32 ∑ ∣ أ⟩∣ب⟩∣ و(أ، ب)⟩ ، حيث f (أ ، ب) = أ + كيلو بايت (وزارة الدفاع 32). أ ، ب 6. سجل نقطة العزل تحتاج الخوارزمية فقط إلى علاقة الطور في أ ، ب. حاجز يعزل ص. 7. تحويل فورييه الكمي (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e ^ ((2πi) / 32 وحدة فلكية) ∣ u ⟩ ، ش = 0 QFT 31 ∣ ب⟩ -> 1/√32 ∑ e ^ ((2πi) / 32 bv) ∣ v⟩. الخامس = 0 8. نمط التداخل سعة المفصل للمراقبة (u ، v) هي: 1/32 ∑_(أ ، ب) e ^ ((2πi / 32) (الاتحاد الأفريقي + BV)) δ_ (أ + كيلو بايت ≡ 0) = 1/32 δ_ (u + kv ≡ 0 (mod 32)) ، والذي يشكل سلسلة من التلال القطرية في شبكة النتائج 32 × 32. 9. القياس قم بقياس جميع الكيوبتات المنطقية العشرة. تركز النتائج على 32 زوجا متميزا ترضي u + kv ≡ 0 (mod 32). 10. المعالجة اللاحقة الكلاسيكية يتم قلب Bitstrings وتحليلها إلى أزواج (أ ، ب). احتفظ فقط بالصفوف حيث gcd (b ، 32) = 1 ، مع التأكد من أن b قابل للعكس. يتم حساب مفتاح المرشح على النحو التالي: ك = (-a) ب ^ (-1) وزارة الدفاع 32 السيناريو إذن: يستخرج أعلى 100 نتيجة قابلة للانعكاس (أ ، ب). يحسب k لكل منهما. يطبع كل زوج (أ ، ب) ، واسترداد k ، والعد. يعلن النجاح إذا ظهر k = 7 في أعلى 100. 11. التحقق والتخزين يتم تأكيد العددي الصحيح k = 7 إذا ظهر في أعلى 100 نتيجة قابلة للعكس. يتم حفظ جميع أعداد سلسلة البتات الأولية وتخطيط الكيوبت وبيانات التعريف في JSON لمزيد من التصور والتحليل. النتائج 2025-06-25 19:41:29,294 | معلومات | عمق الدائرة 67428 ، عدد البوابة OrderedDict ({'sx': 56613 ، 'cz': 34319 ، 'rz': 15355 ، 'x': 157 ، 'measure': 10 ، 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: إرسال الوظيفة باستخدام الخيارات {'options': {}, 'version': 2, 'support_qiskit': True} النجاح - ك = 7 وجدت في أفضل 100 نتيجة أفضل 100 زوج قابل للانعكاس (أ ، ب) واسترداد ك: (أ = 8 ، ب = 11) → ك = 8 (العد = 63) (أ = 12 ، ب = 9) → ك = 20 (العد = 58) (أ = 0 ، ب = 3) → ك = 0 (العد = 54) (أ = 1 ، ب = 9) → ك = 7 (العد = 54) <<< (أ = 28 ، ب = 1) → ك = 4 (العد = 53) (أ = 0 ، ب = 11) → ك = 0 (العد = 53) (أ = 8 ، ب = 9) → ك = 24 (العد = 53) (أ = 8 ، ب = 3) → ك = 8 (العد = 53) ... (أ = 11 ، ب = 3) → ك = 7 (العد = 41) <<< ... (أ = 25 ، ب = 1) → k = 7 (العد = 32) <<< نجح هذا التشغيل في استرداد العددي السري k = 7 باستخدام مفتاح ECC 5 بت (مجموعة فرعية من الترتيب 32) ، مما أدى إلى توسيع هجومي السابق المكون من 4 بت إلى مساحة بها 1024 مجموعة ممكنة (أ ، ب) و φ (32) = 16 قيمة b قابلة للعكس. يظهر k = 7 ثلاث مرات في أعلى 100: (أ = 1 ، ب = 9) -> ك = 7 مع 54 عد (أ = 11 ، ب = 3) -> ك = 7 مع 41 عد (أ = 25 ، ب = 1) -> ك = 7 مع 32 عد هذه حالات عالية التردد ، مما يجعلها نواقل هجوم ذات مصداقية في ظل المعالجة اللاحقة الكلاسيكية. تظهر التهم تركيزا حول العلاقات المعيارية المنظمة: أ + كيلو بايت ≡ 0 تعديل 32. تظهر هذه على شكل حواف قطرية في مساحة القياس 32 × 32. تتكرر العديد من قيم k في كثير من الأحيان (k = 0 ، 24 ، 28) ، مما يدل على التداخل الاحتمالي الجوهري للتداخل الكمي ، وبعضها إيجابي خاطئ من الضوضاء أو التعرج مع معادلات معيارية أخرى. كان عمق الدائرة 67,428 ، بإجمالي 106,455 بوابة ، مما يعكس روتينا كمويا كبيرا ومعقدا لحساب الفهرس المعياري المتحكم فيه. قد يكون هذا أكبر كمية من البوابات التي استخدمتها في الدائرة. عدد البوابات للدائرة: SX: 56613 تشيكوسلوفاكيا: 34319 رتز: 15355 س: 157 القياس: 10 الحاجز: 1 إجمالي البوابات: 106455 العمق: 67428 العرض: 133 كيوبت | 10 كليبت استغرقت هذه التجربة 54 ثانية لإكمالها على "ibm_torino". ملف تعريف الضوضاء غير منتظم ولكنه يتحلل ، مما يعني أن النظام الكمومي من المحتمل أن يحل التوافقيات السائدة في التداخل ولكنه طمس الهياكل الدقيقة. لا يزال ذيل التوزيع يحتوي على k = 7 مرشحين صالحين ، وهذا يدعم الهجمات الكمومية على غرار القاموس حيث تكون عمليات مسح نتائج top-N (N = 100) كافية لاسترداد المفتاح. 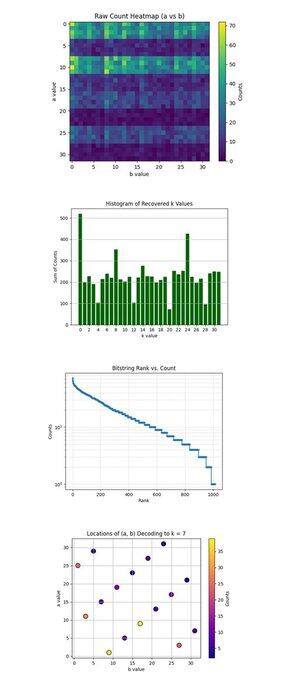تظهر خريطة التمثيل اللوني للعد الخام (a vs b) أعلاه (الكود الكامل على Qwork) شبكة 32 × 32 تمثل الأعداد المرصودة لكل زوج (أ ، ب) بعد تشغيل دائرة شور. تظهر خريطة الحرارة توزيعا مخططا وغير متساو ، مما يشير إلى حواف التداخل ، وليس الضوضاء. تحتوي بعض الصفوف (القيم) على تركيز أعلى بشكل واضح ، مما يشير إلى تداخل بناء على طول حلول محددة من a + kb ≡ 0 mod 32. يجمع الرسم البياني لقيم k المستردة أعلاه (الكود الكامل على Qwork) إجمالي الأعداد لكل مفتاح عددي تم استرداده k ∈ Z₃₂ ، مشتق عبر k = −ab ^ (−1) mod 32. ارتفاع ضخم عند k = 0 وآخر حول k = 24 هو السائد. المفتاح الصحيح k = 7 ليس هو الأعلى ، ولكنه ممثل بشكل جيد (~ 54 + 41 + 32 = 127 عد عبر أزواج متعددة (أ ، ب)). هذا يدل على أن المتسللين يمكنهم مهاجمة قدر أكبر من النتائج. يظهر ترتيب Bitstring مقابل Count (مقياس السجل) أعلاه (الرمز الكامل على Qwork) مخطط رتبة يشبه Zipf لجميع سلاسل البتات عن طريق العد التنازلي. يظهر المحور y ذيل أسي ، وتحدث معظم النتائج <10 مرات. تتميز سلسلة البتات الرئيسية (أعلى ~ 50) باحتمالية أعلى بشكل حاد ، مما يشير إلى قمم التداخل البناء. يمكنك بناء هجوم قاموس إرشادي كمي يحصد فقط أعلى سلاسل بت N مع عائد أسي على الإشارة. هذا يثبت أن بنية الإشارة الكمومية إلى الضوضاء لا تزال سليمة حتى مع الدوائر الأطول (عمق 67428). تظهر مواقع فك التشفير (أ ، ب) إلى k = 7 أعلاه (الكود الكامل على Qwork) أن كل نقطة عبارة عن زوج (أ ، ب) تم فك تشفيره إلى k = 7. كثافة اللون تساوي عدد مرات حدوث هذا الزوج. تظهر المؤامرة توزيعا موحدا نسبيا عبر (أ ، ب) ، ولكن مع قمم محلية عند (1 ، 9) ، (11 ، 3) ، (25 ، 1). تتقارب المجموعات المتعددة (أ ، ب) مع k = 7 مع تعدد غير منتظم. من وجهة نظر تحليل التشفير ، يتحقق هذا من أن خوارزمية Shor يمكنها كسر مفاتيح ECC بشكل موثوق حتى عندما لا يكون k الصحيح هو أعلى 1 نتيجة. 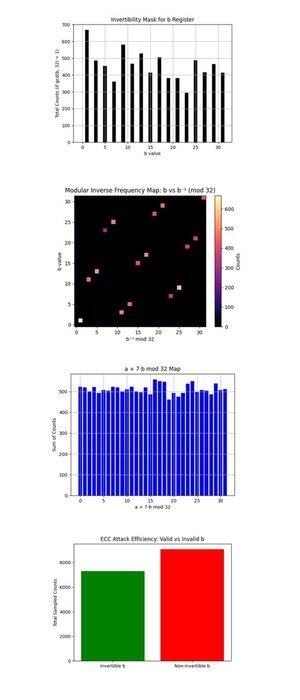يظهر قناع القابلية للانعكاس ل b Register أعلاه (الكود الكامل على Qwork) مخططا شريطيا للأعداد لكل b ∈ {0 ، ... ، 31} التي تكون coprime مع 32 (gcd (b ، 32) = 1 ، فقط هذه هي المعيار القابل للانعكاس 32 ومفيدة لاستعادة k عبر: ك = (−a) ب ^ (−1) mod 32. إن الأجزاء المقلوبة (ب) المكتظة بالسكان بشكل جيد ، مما يدل على أن الدائرة أنتجت مرشحين قابلين للاسترداد. المزيد من التوحيد هنا من شأنه أن يزيد من قوة ما بعد المعالجة ، من الناحية المثالية ، ستكون هذه مسطحة. تظهر خريطة التردد العكسي المعياري: b vs b ^ (−1) mod 32 أعلاه (الكود الكامل على Qwork) خريطة حرارية لعدد المرات التي يتم فيها تعيين كل b قابل للانعكاس إلى كل معكوس معياري مطابق b ^ (−1) mod 32 ، مرجحا بعدد النتائج. تقع معظم النقاط على خط ثنائي نظيف ، كل ب يتم تعيينه بشكل نظيف إلى b ^ (−1) فريد ، مما يؤكد صحة الانعكاس المعياري. تظهر المناطق الأكثر إشراقا (بالقرب من أسفل اليسار أو أعلى اليمين) b المفضلة من أخذ العينات الكمومية. لا ضوضاء أو تجميع خارج قطري ، علامة جيدة على الحفاظ على الهيكل المعياري النظيف. تفترض خريطة a + 7b mod 32 أعلاه (الكود الكامل على Qwork) k = 7 وترسم قيمة (a + 7b) mod 32 عبر جميع النتائج. التوزيع موحد تقريبا. يشير هذا إلى عدم وجود حافة تداخل حادة كما هو الحال في حالة 4 بت. لماذا؟ تنشر الدائرة 5 بت (مع 10 كيوبتات منطقية) أرق السعة عبر 1024 نتيجة ، مما يقلل من التباين. ومع ذلك ، كان المفتاح الصحيح لا يزال قابلا للاسترداد ، مما يشير إلى العديد من المسارات البناءة الضعيفة ، بدلا من عدد قليل من المسارات المهيمنة. كفاءة هجوم ECC: صالح مقابل غير صالح b أعلاه (الرمز الكامل على Qwork) يظهر إجمالي الأعداد من العينات ذات القابل للعكس b (مفيد لاستعادة المفتاح) مقابل غير قابل للعكس b (عديم الفائدة). يتم إهدار أكثر من نصف النتائج على قيم b غير صالحة (gcd (b ، 32) != 1). يمكن أن يستخدم التصميم التالي لفاصل 6 بت إخفاء أوراكل أو تصفية ما بعد التحديد على نطاقات b صالحة. 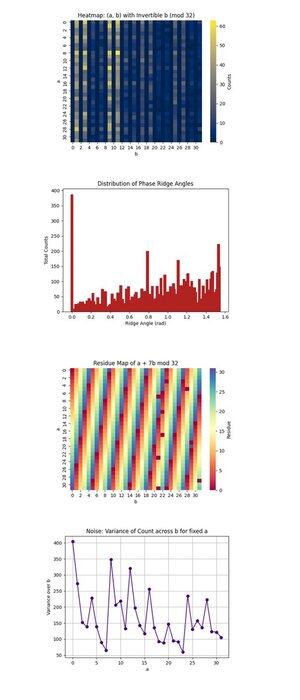خريطة التمثيل الحراري: (أ ، ب) مع انعكاس ب (mod 32) أعلاه (الكود الكامل على Qwork) يركز فقط على أزواج (أ ، ب) حيث يكون b هو المعيار القابل للانعكاس 32 ، وهو شرط ضروري لاستعادة k. يوضح أين يتركز التداخل الكمي داخل مساحة 1024 نقطة. تكشف المناطق عالية الكثافة عن مسارات تداخل مفضلة ، مما يشير إلى أن الحالة الكمومية تطورت بشكل غير موحد ، وربما تفضل مدارات معينة تحت الضرب المعياري. إنه يؤكد تماسك إشارة قوي بما يكفي في بعض المناطق لعزل المرشحين الصالحين توزيع زوايا سلسلة التلال الطورية أعلاه (الكود الكامل على Qwork) يجمع الزوايا التي تشكلت بواسطة متجهات (-a ، b) في المستوى ، modulo π ، والتي تتوافق تقريبا مع حواف الطور في مساحة QFT. تشير القمم في الرسم البياني إلى محاذاة قوية ، رنين ، من النموذج u + kv ≡ 0 ، مما يعني أن الدائرة نجحت في تشفير k في نمط التداخل على الرغم من أن مساحة الحالة الكاملة شاسعة. تشير الزوايا المهيمنة المتعددة إلى وجود توافقيات للتحول الخفي. تصور خريطة المخلفات ل a + 7b mod 32 أعلاه (الكود الكامل على Qwork) بقايا الإخراج للمفتاح المستهدف المحدد k = 7 ، عبر مساحة (a ، b) بأكملها. تشير أي نطاقات أو تماثلات متسقة هنا إلى مدى جودة تضخيم التداخل للحلول الصالحة (حيث تساوي هذه القيمة 0). يمكنك ملاحظة مناطق الشبكة 1024 التي تتوافق مع + 7b ≡ 0 ، مما يؤكد أن بنية أوراكل أدت إلى طباعة مفتاح ناجحة. يوضح الضوضاء: تباين العد عبر b لإصلاح a أعلاه (الرمز الكامل على Qwork) مدى ضجيج أو استقرار عدد المخرجات لكل a ثابت حيث نغير b. يعني التباين العالي أن بعض القيم b تؤدي إلى تضخيم قوي بينما لا يؤدي البعض الآخر إلى ذلك ، مما يعني حساسية الدائرة أو ضوضاء الواجهة الخلفية لهذا الصف a. تشير المناطق الملساء إلى التماسك الكمي ، بينما قد تشير الارتفاعات إلى فك الترابط أو انتشار الخطأ أثناء تقييم أوراكل. في النهاية ، نجحت هذه التجربة في كسر مفتاح منحنى بيضاوي الشكل 5 بت باستخدام خوارزمية شور المنفذة على معالج IBM الكمي 133 كيوبت ، مما أدى إلى توسيع النتيجة السابقة المكونة من 4 بت إلى مساحة تداخل أكبر بكثير (32 × 32 = 1024 نتيجة). قامت هذه الدائرة بتشفير أوراكل عبر Z₃₂ دون الرجوع إلى العددي السري k ، واستفدت من حساب المجموعة المعيارية لتشابك العددي في تداخل الطور. أنتجت الدائرة الكمومية ، التي يزيد عمقها عن 67,000 طبقة ، أنماط تداخل صالحة على الرغم من عمق الدائرة الشديد ، وكشفت المعالجة اللاحقة الكلاسيكية k = 7 في أفضل 100 نتيجة قابلة للعكس (أ ، ب). من خلال التصورات ، أكدت هذه التجربة هياكل التلال القطرية ، وأقنعة الانعكاس ، والمحاذاة التوافقية لحواف التداخل ، مما يؤكد أن التماسك الكمي ظل قويا بما يكفي لتضخيم العلاقة المعيارية الصحيحة. هذا يثبت أن خوارزمية شور تستمر في التوسع في ظل أنظمة الدوائر الأعمق وأن استراتيجيات استرداد المفاتيح القائمة على القاموس (أعلى 100 تعداد) تظل قابلة للتطبيق مع زيادة طول البتات ، مما يدل على ميزة كمية واضحة حتى في ظل ظروف العالم الحقيقي الصاخبة. رمز # الدائرة الرئيسية # الواردات استيراد التسجيل, JSON من استيراد الرياضيات GCD استيراد numpy ك NP من qiskit استيراد QuantumCircuit ، QuantumRegister ، ClassicalRegister ، transpile من qiskit.circuit.library استيراد UnitaryGate ، QFT من qiskit_ibm_runtime استيراد QiskitRuntimeService, SamplerV2 استيراد الباندا بتنسيق PD # آي بي إم كيو رمز مميز = "YOUR_IBMQ_API_KEY" INSTANCE = "YOUR_IBMQ_CRN" الواجهة الخلفية = "ibm_torino" CAL_CSV = "/المستخدمون/steventippeconnic/التنزيلات/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" اللقطات = 16384 # معلمات منحنى اللعبة (المجموعة الفرعية للترتيب 32 من E (F_p)) الطلب = 32 # |ه(F_p)| = 32 P_IDX = 1 # مولد P -> مؤشر 1 Q_IDX = 23 # النقطة العامة Q = kP ، هنا "23 mod 32" ل k = 7 # مساعد التسجيل logging.basicConfig (المستوى = تسجيل .INFO ، format="٪(asctime)s | ٪(levelname)s | ٪ (رسالة)s") log = logging.getLogger(__name__) # اختيار الكيوبت القائم على المعايرة def best_qubits(csv_path: str, n: int) -> list[int]: DF = PD .read_csv(csv_path) df.columns = df.columns.str.strip () الفائزون = ( df.sort_values(["خطأ √x (sx)" ، "T1 (لنا)" ، "T2 (لنا)"] ، تصاعدي = [صواب ، خطأ ، خطأ]) ["كيوبت"].head(n).tolist() ) log .info("أفضل الكيوبتات المادية: ٪s"، الفائزين) الفائزون العائدون N_Q = 5 N_Q_TOTAL = N_Q * 3 # أ ، ب ، نقطة مادي = best_qubits (CAL_CSV ، N_Q_TOTAL) # modulo الأفعى الثابتة 32 كبوابة قابلة لإعادة الاستخدام def add_const_mod32_gate(c: int) -> UnitaryGate: """"إرجاع بوابة 5 كيوبت ترسم خرائط |x⟩ ↦ |x + c (mod 32)⟩""" حصيرة = np.أصفار ((32 ، 32)) ل x في النطاق (32): حصيرة [(x + c) ٪ 32 ، x] = 1 إرجاع UnitaryGate (حصيرة ، تسمية = f "+ {c}") ADDERS = {c: add_const_mod32_gate(c) ل c في النطاق (1 ، 32)} def controlled_add (qc: QuantumCircuit ، ctrl_qubit ، point_reg ، ثابت): """تطبيق |x⟩ → |x + ثابت (mod 32)⟩ يتم التحكم فيه بواسطة كيوبت واحد.""" qc.append(ADDERS[constant].control()، [ctrl_qubit، *point_reg]) # أوراكل U_f: |أ⟩|ب⟩|0⟩ ⟶ |أ⟩|ب⟩|aP + bQ⟩ (الفهرس الحسابي mod 32) ديف ecdlp_oracle (مراقبة الجودة ، a_reg ، b_reg ، point_reg): ل I في النطاق (N_Q): ثابت = (P_IDX * (1 << i)) ٪ ترتيب إذا كان ثابتا: controlled_add (مراقبة الجودة ، a_reg [i] ، point_reg ، ثابت) ل I في النطاق (N_Q): ثابت = (Q_IDX * (1 << i)) ٪ ترتيب إذا كان ثابتا: controlled_add(qc ، b_reg [i] ، point_reg ، ثابت) # قم ببناء دائرة Shor الكاملة def shor_ecdlp_circuit() -> QuantumCircuit: أ = QuantumRegister (N_Q ، "أ") ب = QuantumRegister (N_Q ، "ب") ع = QuantumRegister (N_Q ، "p") ج = ClassicalRegister (N_Q * 2 ، "c") qc = QuantumCircuit (أ ، ب ، ع ، ج ، الاسم = "ECDLP_32pts") QC.H(أ) مراقبة الجودة (ب) ecdlp_oracle (مراقبة الجودة ، أ ، ب ، ع) QC.barrier() qc.append(QFT(N_Q، do_swaps=خطأ)، أ) qc.append(QFT(N_Q، do_swaps=خطأ)، ب) قياس الجودة (أ ، ج [: N_Q]) قياس الجودة (ب ، ج [N_Q:]) عودة مراقبة الجودة # تنفيذ IBM Runtime service = QiskitRuntimeService(channel="ibm_cloud", رمز مميز = رمز مميز ، instance=INSTANCE) الواجهة الخلفية = service.backend (الواجهة الخلفية) log .info("الواجهة الخلفية → ٪s", الواجهة الخلفية .name) qc_raw = shor_ecdlp_circuit() عبر = transpile (qc_raw ، الواجهة الخلفية = الخلفية ، initial_layout = المادية ، optimization_level = 3) log .info("عمق الدائرة٪d، عدد البوابة ٪s"، trans.depth()، trans.count_ops()) أخذ العينات = SamplerV2 (الوضع = الواجهة الخلفية) الوظيفة = أخذ العينات .run ([عبر] ، اللقطات = اللقطات) النتيجة = job.result() # المعالجة اللاحقة الكلاسيكية creg_name = trans.cregs[0].name counts_raw = النتيجة[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(BS): إرجاع int (BS [::-1] ، 2) التهم = {(bits_to_int(ك [N_Q:]) ، bits_to_int (ك [: N_Q])): v ل k ، v في counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse = true) # معايير النجاح. تحقق من أفضل 100 صف قابل للانعكاس ل k = 7 top_invertibles = [] بالنسبة إلى (a_val ، b_val) ، التردد في الأعلى: إذا كان gcd(b_val، ORDER) != 1: استمر inv_b = أسرى الحرب (b_val ، -1 ، أمر) k_candidate = (-a_val * inv_b) ٪ طلب top_invertibles.append(((a_val ، b_val) ، k_candidate ، freq)) إذا كان len(top_invertibles) == 100: كسر # تحقق من النجاح وطباعة النتائج found_k7 = any(k == 7 ل (_ ، k ، _) في top_invertibles) إذا found_k7: print("\nSUCCESS - k = 7 وجدت في أفضل 100 نتيجة \n") اخر: print("\nتحذير - k = 7 غير موجود في أفضل 100 نتيجة \n") print("أفضل 100 زوج قابل للانعكاس (أ ، ب) واسترداد k :") بالنسبة إلى (أ ، ب) ، ك ، العد في top_invertibles: علامة = " <<<" إذا كان k == 7 آخر "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count}){tag}") # حفظ البيانات الأولية خارج = { "experiment": "ECDLP_32pts_Shors", "الواجهة الخلفية": الواجهة الخلفية .name، "physical_qubits": جسدي، "اللقطات": طلقات ، "التهم": counts_raw } JSON_PATH = "/المستخدمون / steventippeconnic / المستندات / مراقبة الجودة / Shors_ECC_5_Bit_Key_0.json" مع open(JSON_PATH, "w") ك fp: json.dump (مخرج ، FP ، مسافة بادئة = 4) log .info("النتائج المحفوظة →٪s", JSON_PATH) # النهاية كود كامل لجميع المرئيات باستخدام بيانات التشغيل على Qwork.