Een 5-Bit Elliptische Curvesleutel kraken met een 133-Qubit Quantumcomputer ⚛️ Dit experiment kraakt een 5-bit elliptische curve cryptografische sleutel met behulp van Shor's algoritme. Uitgevoerd op @IBM's 133-qubit ibm_torino met @qiskit, interfereert een 15-qubit circuit, bestaande uit 10 logische qubits en 5 ancilla, over ℤ₃₂ om de geheime scalair k uit de publieke sleutelrelatie Q = kP te extraheren, zonder k ooit direct in de oracle te coderen. Van de 16.384 shots onthult de kwantuminterferentie een diagonale kam in de 32x32 QFT-uitkomstruimte. Het kwantumcircuit, meer dan 67.000 lagen diep, produceerde geldige interferentiepatronen ondanks de extreme circuitdiepte, en klassieke post-processing onthulde k = 7 in de top 100 omkeerbare (a, b) resultaten. Code Walkthrough 1. Groep Codering Beperk de aandacht tot de orde-32 subgroep ⟨𝑃⟩ van een elliptische curve over 𝐹_p. Map punten naar gehele getallen: 0𝑃 -> 0,  1𝑃 -> 1, …, 31𝑃 -> 31. De groepswet wordt modulair optellen: (𝑥𝑃) + (𝑦𝑃) = ((𝑥 + 𝑦) mod 32))𝑃. Dit experiment gebruikt een elliptische curve over F_p​ met een cyclische subgroep van orde 32, waarbij P -> 1 en Q = 7P -> 23 in ℤ₃₂​ wordt gemapt. De code gaat uit van vooraf berekende scalair vermenigvuldiging, waarbij expliciete coördinaten worden geabstraheerd. 2. Kwantum Registers Register a: vijf qubits voor de exponent 𝑎 ∈ {0, …, 31}. Register b: vijf qubits voor 𝑏 ∈ {0, …, 31}. Register p: vijf qubits geïnitialiseerd op ∣0⟩ om de puntindex vast te houden. Klassiek register c: een 10-bit register om de gemeten waarden van a en b vast te leggen. 3. Superpositie Voorbereiding Pas Hadamards toe op elke qubit in a en b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Oracle constructie U_f Doel is een omkeerbare kaart: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Voeg aP toe: voor elke bit a_i (gewicht 2^𝑖), voeg (2^𝑖 P) mod 32 toe. Voeg bQ toe: bereken (2^𝑖 𝑄) mod 32, voeg dan gecontroleerd toe op 𝑏_𝑖. Deze gebruiken 5-qubit gecontroleerde permutatiepoorten. Alle constanten zijn afgeleid van de generator P van de elliptische curve en het publieke punt Q. Geen poort verwijst ooit direct naar de geheime k. 5. Globale Toestand na Oracle De toestand evolueert naar: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, waar f(a, b) = a + kb (mod32). a, b 6. Isoleren Punt Register Het algoritme heeft alleen de fase-relatie in 𝑎, 𝑏 nodig. Een barrière isoleert p. 7. Kwantum Fourier Transformatie (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Interferentiepatroon De gezamenlijke amplitude voor het observeren van (u, v) is: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), wat een diagonale kam in het 32x32 uitkomstrooster vormt. 9. Meting Meet alle tien logische qubits. Uitkomsten concentreren zich op de 32 verschillende paren die voldoen aan u + kv ≡ 0 (mod 32). 10. Klassieke Post-Processing Bitstrings worden endian-flipped en geparsed in (a, b) paren. Behoud alleen rijen waar gcd⁡(b, 32) = 1, zodat b omkeerbaar is. De kandidaat sleutel wordt berekend als: k = (-a) b^(-1) mod 32 Het script: Extracteert de top 100 hoogste-telling omkeerbare (a, b) resultaten. Bereken k voor elk. Print elk (a, b) paar, herstelde k, en telling. Verklaart succes als k = 7 voorkomt in de top 100. 11. Verificatie en Opslag De correcte scalair k = 7 wordt bevestigd als het voorkomt in de top 100 omkeerbare resultaten. Alle ruwe bitstring tellingen, qubit lay-out, en metadata worden opgeslagen in JSON voor verdere visualisatie en analyse. Resultaten 2025-06-25 19:41:29,294 | INFO | Circuitdiepte 67428, poorttelling OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'meet': 10, 'barrière': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Taak indienen met opties {'options': {}, 'version': 2, 'support_qiskit': True} SUCCES — k = 7 gevonden in de top 100 resultaten Top 100 omkeerbare (a, b) paren en herstelde k: (a= 8, b=11) → k = 8 (telling = 63) (a=12, b= 9) → k = 20 (telling = 58) (a= 0, b= 3) → k = 0 (telling = 54) (a= 1, b= 9) → k = 7 (telling = 54) <<< (a=28, b= 1) → k = 4 (telling = 53) (a= 0, b=11) → k = 0 (telling = 53) (a= 8, b= 9) → k = 24 (telling = 53) (a= 8, b= 3) → k = 8 (telling = 53) ... (a=11, b= 3) → k = 7 (telling = 41) <<< ... (a=25, b= 1) → k = 7 (telling = 32) <<< Deze run heeft met succes de geheime scalair k = 7 hersteld met behulp van een 5-bit ECC sleutel (orde-32 subgroep), waarmee mijn eerdere 4-bit aanval werd uitgebreid naar een ruimte met 1024 mogelijke (a, b) combinaties en φ(32) = 16 omkeerbare b-waarden. k = 7 verschijnt drie keer in de top 100: (a = 1, b = 9) -> k = 7 met 54 tellingen (a = 11, b = 3) -> k = 7 met 41 tellingen (a =25, b = 1) -> k = 7 met 32 tellingen Dit zijn hoogfrequente toestanden, waardoor ze geloofwaardige aanvalsvectors zijn onder klassieke post-processing. De tellingen vertonen concentratie rond gestructureerde modulaire relaties: a + kb ≡ 0 mod 32. Deze verschijnen als diagonale kammen in de 32x32 meetruimte. Verschillende k-waarden komen vaak voor (k = 0, 24, 28), wat de probabilistische overlap toont die intrinsiek is aan kwantuminterferentie, sommige hiervan zijn valse positieven door ruis of aliasing met andere modulaire equivalenties. De circuitdiepte was 67.428, met een totaal van 106.455 poorten, wat een grote, complexe kwantumroutine voor gecontroleerde modulaire indexarithmetic weerspiegelt. Dit kan de grootste hoeveelheid poorten zijn die ik in een circuit heb gebruikt. Poorttelling voor het circuit: sx: 56613 cz: 34319 rz: 15355 x: 157 meet: 10 barrière: 1 Totaal aantal poorten: 106455 Diepte: 67428 Breedte: 133 qubits | 10 clbits Dit experiment duurde 54 seconden om te voltooien op 'ibm_torino'. Het ruisprofiel is niet-uniform maar afnemend, wat betekent dat het kwantumsysteem waarschijnlijk dominante harmonischen in de interferentie heeft opgelost maar fijnere structuren heeft vervaagd. De distributietail bevat nog steeds geldige k = 7 kandidaten, dit ondersteunt dictionary-stijl kwantumaanvallen waarbij scans van top-N resultaten (N = 100) voldoende zijn om de sleutel te herstellen. 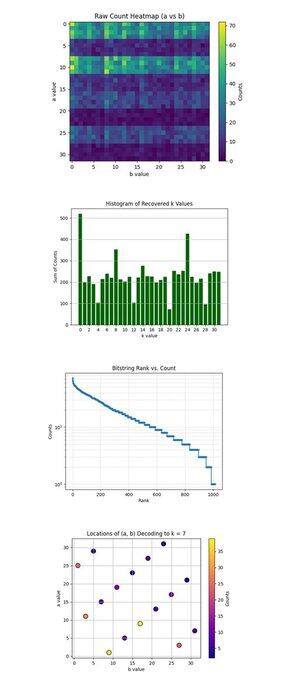De Ruwe Telling Heatmap (a vs b) hierboven (volledige code op Qwork) toont een 32x32 rooster dat de waargenomen tellingen voor elk paar (a, b) weergeeft na het uitvoeren van Shor's circuit. De heatmap toont een banded en ongelijke distributie, wat interferentieridges aangeeft, geen ruis. Bepaalde rijen (a-waarden) hebben zichtbaar hogere concentratie, wat constructieve interferentie langs specifieke a + kb ≡ 0 mod 32 oplossingen suggereert. De Histogram van Herstelde k Waarden hierboven (volledige code op Qwork) aggregeert de totale tellingen voor elke herstelde scalair sleutel k ∈ Z₃₂, afgeleid via k = −ab^(−1) mod 32. Een enorme piek bij k = 0 en een andere rond k = 24 zijn dominant. De correcte sleutel k = 7 is niet de hoogste, maar is goed vertegenwoordigd (~54 + 41 + 32 = 127 tellingen over meerdere (a, b) paren). Dit toont aan dat hackers een dictionary-aanval kunnen uitvoeren op een groter aantal resultaten. De Bitstring Rang vs Telling (Log-Schaal) hierboven (volledige code op Qwork) toont een Zipf-achtige rangplot van alle bitstrings op basis van aflopende telling. De log-schaal y-as toont een exponentiële staart, de meeste uitkomsten komen <10 keer voor. De kop (top ~50) bitstrings hebben steil hogere waarschijnlijkheid, wat constructieve interferentiepieken aangeeft. Je zou een kwantumheuristische dictionary-aanval kunnen bouwen die alleen de top N bitstrings met exponentieel rendement op signaal verzamelt. Dit valideert dat de kwantum signaal-ruisstructuur nog steeds intact is, zelfs met langere circuits (67428 diepte). De Locaties van (a, b) Decodering naar k = 7 hierboven (volledige code op Qwork) toont dat elke stip een (a, b) paar is dat naar k = 7 decodering. Kleurintensiteit is gelijk aan het aantal keren dat dit paar is voorgekomen. De plot toont een relatief uniforme distributie over (a, b), maar met lokale pieken bij (1, 9), (11, 3), (25, 1). Meerdere (a, b) combinaties convergeren naar k = 7 met niet-uniforme multipliciteit. Vanuit een cryptanalytisch standpunt valideert dit dat Shor's algoritme betrouwbaar ECC-sleutels kan kraken, zelfs wanneer de juiste k niet de top 1 resultaat is. 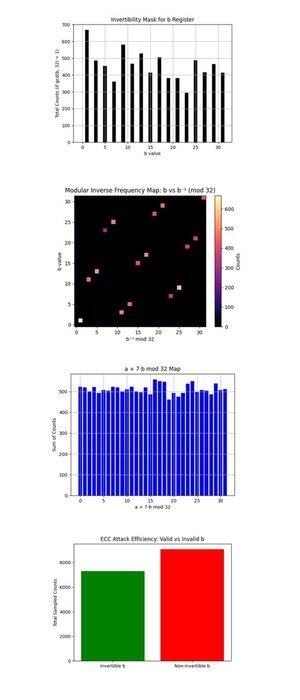De Omkeerbaarheid Masker voor b Register hierboven (volledige code op Qwork) toont een staafdiagram van tellingen voor elke b ∈ {0, …, 31} die coprime zijn met 32 (gcd⁡(b, 32) = 1, alleen deze zijn omkeerbaar modulo 32 en nuttig voor het herstellen van k via: k = (−a)b^(−1) mod 32. Omkeerbare b's zijn goed bevolkt, wat aangeeft dat het circuit herstellende kandidaten heeft geproduceerd. Meer uniformiteit hier zou de post-processing kracht vergroten, idealiter zouden deze vlak zijn. De Modulaire Inverse Frequentiekaart: b vs b^(−1) mod 32 hierboven (volledige code op Qwork) toont een heatmap van hoe vaak elke omkeerbare b naar elke bijbehorende modulaire inverse b^(−1) mod 32, gewogen door resultaat tellingen. De meeste punten vallen op een schone bijectieve lijn, elke b map schoon naar een unieke b^(−1), wat de correctheid van modulaire inversie bevestigt. Heldere gebieden (dicht bij de linksonder of rechtboven) tonen bevoordeelde b's van de kwantummonsters. Geen off-diagonale ruis of clustering, goed teken van schone modulaire structuur behouden. De a + 7b mod 32 Kaart hierboven (volledige code op Qwork) gaat ervan uit dat k = 7 en plot de waarde van (a + 7b) mod 32 over alle resultaten. De distributie is bijna uniform. Dit suggereert geen scherpe interferentieridge zoals in het 4-bit geval. Waarom? Het 5-bit circuit (met 10 logische qubits) verspreidt amplitude dunner over 1024 uitkomsten, waardoor het contrast vermindert. Toch was de juiste sleutel nog steeds herstellend, wat aangeeft dat er veel zwak constructieve paden zijn, in plaats van een paar dominante. De ECC Aanvalsefficiëntie: Geldige vs Ongeldige b hierboven (volledige code op Qwork) toont totale tellingen van monsters met omkeerbare b (nuttig voor sleutelherstel) vs. niet-omkeerbare b (nuttig). Meer dan de helft van de resultaten zijn verspild aan ongeldige b-waarden (gcd⁡(b, 32) != 1). Het volgende ontwerp voor een 6-bit doorbraak zou oracle masking of postselectief filteren op geldige b-domeinen kunnen gebruiken. 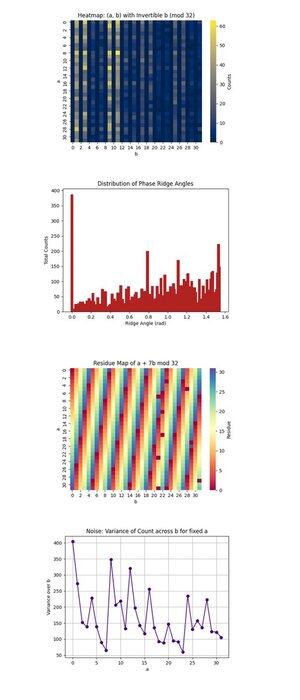De Heatmap: (a, b) met Omkeerbare b (mod 32) hierboven (volledige code op Qwork) richt zich alleen op (a, b) paren waarbij b omkeerbaar is modulo 32, een noodzakelijke voorwaarde voor het herstellen van k. Het toont waar kwantuminterferentie zich concentreert binnen de 1024-punt ruimte. De hoog-intensiteitsgebieden onthullen voorkeur interferentie paden, wat suggereert dat de kwantumtoestand niet-uniform is geëvolueerd, mogelijk bepaalde banen onder modulaire vermenigvuldiging bevoordigend. Het bevestigt sterke genoeg signaalcoherentie in sommige gebieden om geldige kandidaten te isoleren. De Distributie van Fasekam Hoeken hierboven (volledige code op Qwork) bin de hoeken gevormd door (-a, b) vectoren in het vlak, modulo π, die ruwweg overeenkomen met fasekammen in de QFT-ruimte. Pieken in de histogram geven sterke uitlijningen, resonanties aan van de vorm u + kv ≡ 0, wat betekent dat het circuit met succes k in het interferentiepatroon heeft gecodeerd, ook al is de volledige toestandsruimte enorm. De meerdere dominante hoeken suggereren dat harmonischen van de verborgen verschuiving aanwezig zijn. De Restkaart van a + 7b mod 32 hierboven (volledige code op Qwork) visualiseert de outputrest voor de specifieke doel sleutel k = 7, over de gehele (a, b) ruimte. Consistente banden of symmetrieën hier geven aan hoe goed de interferentie geldige oplossingen heeft versterkt (waar deze waarde gelijk is aan 0). Je kunt observeren welke gebieden van de 1024 rooster overeenkomen met a + 7b ≡ 0, wat valideert dat de structuur van de oracle leidde tot succesvolle sleutelafdrukken. De Ruis: Variantie van Telling over b voor vaste a hierboven (volledige code op Qwork) toont hoe ruisachtig of stabiel de outputtelling was voor elke vaste a terwijl we b variëren. Hoge variantie betekent dat sommige b-waarden leiden tot sterke versterking terwijl andere dat niet doen, wat circuitgevoeligheid of backendruis voor die a-rij impliceert. Vlotte gebieden impliceren kwantumcoherentie, terwijl pieken kunnen wijzen op decoherentie of foutpropagatie tijdens oracle-evaluatie. Uiteindelijk heeft dit experiment met succes een 5-bit elliptische curve sleutel gekraakt met behulp van Shor's algoritme uitgevoerd op IBM's 133-qubit quantumprocessor, waarmee het eerdere 4-bit resultaat werd uitgebreid naar een aanzienlijk grotere interferentieruimte (32x32 = 1024 uitkomsten). Dit circuit codeerde de oracle over ℤ₃₂ zonder ooit de geheime scalair k te verwijzen, en maakte gebruik van modulaire groepsarithmetic om de scalair in fase-interferentie te verstrengelen. Het kwantumcircuit, meer dan 67.000 lagen diep, produceerde geldige interferentiepatronen ondanks de extreme circuitdiepte, en klassieke post-processing onthulde k = 7 in de top 100 omkeerbare (a, b) resultaten. Door visualisaties bevestigde dit experiment diagonale kamstructuren, omkeerbaarheid maskers, en harmonische uitlijning van interferentieridges, wat valideert dat kwantumcoherentie sterk genoeg bleef om de juiste modulaire relatie te versterken. Dit stelt vast dat Shor's algoritme blijft schalen onder diepere circuitregimes en dat dictionary-gebaseerde sleutelherstelstrategieën (top 100 enumeratie) levensvatbaar blijven naarmate de bitlengte toeneemt, wat een duidelijke kwantumvoordeel toont, zelfs onder ruisachtige omstandigheden in de echte wereld. Code # Hoofd circuit # Imports import logging, json from math import gcd import numpy as np from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile from qiskit.circuit.library import UnitaryGate, QFT from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2 import pandas as pd # IBMQ TOKEN = "YOUR_IBMQ_API_KEY" INSTANCE = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" SHOTS = 16384 # Toy‑curve parameters (orde‑32 subgroep van E(F_p)) ORDER = 32 # |E(F_p)| = 32 P_IDX = 1 # Generator P -> index 1 Q_IDX = 23 # Publieke punt Q = kP, hier “23 mod 32” voor k = 7 # Logging helper logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(levelname)s | %(message)s") log = logging.getLogger(__name__) # Calibration‑based qubit pick def best_qubits(csv_path: str, n: int) -> list[int]: df = pd .read_csv(csv_path) df.columns = df.columns.str.strip() winners = ( df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"], ascending=[True, False, False]) ["Qubit"].head(n).tolist() ) log .info("Beste fysieke qubits: %s", winners) return winners N_Q = 5 N_Q_TOTAL = N_Q * 3 # a, b, punt PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL) # Constant-adder modulo 32 als een herbruikbare poort def add_const_mod32_gate(c: int) -> UnitaryGate: """Retourneer een 5‑qubit poort die |x⟩ ↦ |x+c (mod 32)⟩.""" mat = np.zeros((32, 32)) for x in range(32): mat[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant): """Pas |x⟩ → |x+constant (mod 32)⟩ gecontroleerd door één qubit toe.""" qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg]) # Oracle U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (index arithmetic mod 32) def ecdlp_oracle(qc, a_reg, b_reg, point_reg): for i in range(N_Q): constant = (P_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, a_reg[i], point_reg, constant) for i in range(N_Q): constant = (Q_IDX * (1 << i)) % ORDER if constant: controlled_add(qc, b_reg[i], point_reg, constant) # Bouw het volledige Shor circuit def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(qc, a, b, p) qc.barrier() qc.append(QFT(N_Q, do_swaps=False), a) qc.append(QFT(N_Q, do_swaps=False), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) return qc # IBM Runtime uitvoering service = QiskitRuntimeService(channel="ibm_cloud", token=TOKEN, instance=INSTANCE) backend = service.backend(BACKEND) log .info("Backend → %s", backend .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend=backend, initial_layout=PHYSICAL, optimization_level=3) log .info("Circuitdiepte %d, poorttelling %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(mode=backend) job = sampler .run([trans], shots=SHOTS) result = job.result() # Klassieke post‑processing creg_name = trans.cregs[0].name counts_raw = result[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): return int(bs[::-1], 2) counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v for k, v in counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Succescriteria. Controleer de top 100 omkeerbare rijen voor k = 7 top_invertibles = [] for (a_val, b_val), freq in top: if gcd(b_val, ORDER) != 1: continue inv_b = pow(b_val, -1, ORDER) k_candidate = (-a_val * inv_b) % ORDER top_invertibles.append(((a_val, b_val), k_candidate, freq)) if len(top_invertibles) == 100: break # Controleer op succes en print resultaten found_k7 = any(k == 7 for (_, k, _) in top_invertibles) if found_k7: print("\nSUCCES — k = 7 gevonden in de top 100 resultaten\n") else: print("\nWAARSCHUWING — k = 7 NIET gevonden in de top 100 resultaten\n") print("Top 100 omkeerbare (a, b) paren en herstelde k:") for (a, b), k, count in top_invertibles: tag = " <<<" if k == 7 else "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (telling = {count}){tag}") # Sla ruwe gegevens op out = { "experiment": "ECDLP_32pts_Shors", "backend": backend .name, "fysieke_qubits": PHYSICAL, "shots": SHOTS, "counts": counts_raw } JSON_PATH = "/Users/steventippeconnic/Documents/QC/Shors_ECC_5_Bit_Key_0.json" with open(JSON_PATH, "w") as fp: json.dump(out, fp, indent=4) log .info("Resultaten opgeslagen → %s", JSON_PATH) # Einde Volledige code voor alle visualisaties met behulp van run gegevens op Qwork.