Розбиття 5-бітного ключа еліптичної кривої за допомогою 133-кубітного квантового комп'ютера ⚛️ Цей експеримент розбиває криптографічний ключ з 5-бітною еліптичною кривою за допомогою алгоритму Шора. Виконана на 133-кубітній ibm_torino @IBM з @qiskit, 15-кубітна схема, що складається з 10 логічних кубітів і 5 допоміжних, втручається в Z₃₂, щоб витягнути секретний скаляр k з відношення відкритих ключів Q = kP, ніколи не кодуючи k безпосередньо в оракул. З 16 384 знімків квантова інтерференція виявляє діагональний гребінь у вихідному просторі 32x32 QFT. Квантова схема, глибиною понад 67 000 шарів, створювала дійсні інтерференційні картини, незважаючи на екстремальну глибину ланцюга, а класична постобробка показала k = 7 у топ-100 обернених (a, b) результатів. Проходження коду 1. Кодування груп Обмежте увагу підгрупою порядку 32 ⟨Р⟩ еліптичної кривої над F_p. Карта вказує на цілі числа: 0П -> 0, 1П -> 1, ..., 31П -> 31. Групове право набуває модульного доповнення: (xP) + (yP) = ((x + y) mod 32))P. У цьому експерименті використовується еліптична крива над F_p з циклічною підгрупою порядку 32, відображаючи P -> 1 і Q = 7P -> 23 в Z₃₂. Код передбачає попередньо обчислене скалярне множення, абстрагування явних координат. 2. Квантові регістри Регістр a: п'ять кубітів для показника степеня a ∈ {0, ..., 31}. Регістр b: п'ять кубітів для b ∈ {0, ..., 31}. Регістр p: п'ять кубітів ініціалізуються на ∣0⟩ для утримання індексу точок. Класичний регістр c: 10-розрядний регістр для запису виміряних значень a і b. 3. Підготовка до суперпозиції Застосуйте Гадамарди до кожного кубіта в a і b: 31 1/32 ∑ ∣a⟩_a ∣b⟩_b ∣0⟩_p a, b=0 4. Будівництво оракула U_f Мета – це обернена карта: ∣a⟩ ∣b⟩ ∣0⟩ -> ∣a⟩ ∣b⟩ ∣aP + bQ⟩. Додати aP: для кожного біта a_i (вага 2^i) додати (2^i P) mod 32 Додайте bQ: обчисліть (2^i Q) mod 32, а потім додайте контрольовані на b_i. У них використовуються 5-кубітні керовані вентилі перестановки. Всі константи є похідними від генератора P еліптичної кривої і відкритої точки Q. Жодні ворота ніколи прямо не посилаються на таємницю к. 5. Глобальна держава після Oracle Держава еволюціонує в: 1/32 ∑ ∣a⟩∣b⟩∣f(a, b)⟩, де f(a, b) = a + kb (mod32). А, Б 6. Ізолюйте точковий регістр Алгоритму потрібна тільки співвідношення фаз в a, b. Бар'єр ізолює п. 7. Квантове перетворення Фур'є (QFT) QFT 31 ∣a⟩ -> 1/√32 ∑ e^((2πi)/32 au) ∣u⟩, u=0 QFT 31 ∣b⟩ -> 1/√32 ∑ e^((2πi)/32 bv) ∣v⟩. v=0 8. Інтерференційна картина Амплітуда суглобів для спостереження (u, v) становить: 1/32 ∑_(a, b) e^((2πi/32)(au + bv)) δ_(a + kb ≡ 0) = 1/32 δ_(u + kv ≡ 0 (mod 32)), що утворює діагональний гребінь у сітці результатів 32x32. 9. Вимірювання Виміряйте всі десять логічних кубітів. Результати концентруються на 32 різних парах, що задовольняють u + kv ≡ 0 (mod 32). 10. Класична постобробка Бітові рядки перевертаються ендіаном і розбираються на пари (a, b). Зберігайте лише рядки, де НСД(b, 32) = 1, забезпечуючи оберненість b. Потенційний ключ обчислюється як: k = (-a) b^(-1) mod 32 Тоді сценарій: Витягує 100 найкращих інвертованих результатів (a, b) з найбільшою кількістю. Обчислює k для кожного. Виводить кожну пару (a, b), відновлену k і count. Оголошує про успіх, якщо k = 7 з'являється в топ-100. 11. Перевірка та зберігання Правильний скаляр k = 7 підтверджується, якщо він з'являється в топ-100 обернених результатів. Усі необроблені кількості бітових рядків, макет кубіта та метадані зберігаються в JSON для подальшої візуалізації та аналізу. Результатів 2025-06-25 19:41:29,294 | ІНФО | Глибина ланцюга 67428, кількість воріт OrderedDict({'sx': 56613, 'cz': 34319, 'rz': 15355, 'x': 157, 'measure': 10, 'barrier': 1}) base_primitive._run:INFO:2025-06-25 19:41:29,994: Надсилання завдання за допомогою опцій {'options': {}, 'version': 2, 'support_qiskit': True} УСПІХ — k = 7 знайдено в топ-100 результатів Топ-100 обернених (a, b) пар і відновлених k: (А = 8, Б = 11) → К = 8 (кількість = 63) (А = 12, Б = 9) → К = 20 (кількість = 58) (a= 0, b= 3) → k = 0 (кількість = 54) (А = 1, Б = 9) → К = 7 (кількість = 54) <<< (А = 28, Б = 1) → К = 4 (кількість = 53) (a= 0, b=11) → k = 0 (кількість = 53) (А = 8, Б = 9) → К = 24 (кількість = 53) (А = 8, Б = 3) → К = 8 (кількість = 53) ... (А = 11, Б = 3) → К = 7 (кількість = 41) <<< ... (a=25, b= 1) → k = 7 (кількість = 32) <<< Цей запуск успішно отримав секретний скаляр k = 7 за допомогою 5-бітного ECC-ключа (підгрупа order-32), розширивши мою попередню 4-бітну атаку на пробіл з 1024 можливими (a, b) комбінаціями та φ(32) = 16 оберненими значеннями b. k = 7 з'являється в топ-100 тричі: (a = 1, b = 9) -> k = 7 з 54 рахунками (а = 11, б = 3) -> к = 7 з 41 рахунком (а = 25, б = 1) -> к = 7 з 32 рахунками Це високочастотні стани, що робить їх вірогідними векторами атак при класичній постобробці. Підрахунки демонструють концентрацію навколо структурованих модульних відносин: a + kb ≡ 0 mod 32. Вони виглядають як діагональні гребені в просторі вимірювання 32x32. Кілька значень k часто повторюються (k = 0, 24, 28), демонструючи імовірнісне перекриття, властиве квантовій інтерференції, деякі з них є помилковими спрацьовуваннями від шуму або псевдонімації з іншими модульними еквівалентностями. Глибина ланцюга становила 67 428, із загальною кількістю 106 455 вентилів, що відображає велику, складну квантову рутину для арифметики керованих модульних індексів. Можливо, це найбільша кількість вентилів, яку я використовував у схемі. Кількість воріт для ланцюга: грн.: 56613 CZ: 34319 РЗ: 15355 х: 157 міра: 10 Бар'єр: 1 Всього воріт: 106455 Глибина: 67428 Ширина: 133 кубіти | 10 бітів Цей експеримент зайняв 54 секунди на «ibm_torino». Профіль шуму неоднорідний, але затухає, що означає, що квантова система, швидше за все, розв'язала домінуючі гармоніки в інтерференції, але розмила більш тонкі структури. Хвіст розподілу все ще містить дійсні k = 7 кандидатів, це підтримує квантові атаки в стилі словника, де сканування результатів зверху N (N = 100) достатньо, щоб отримати ключ. 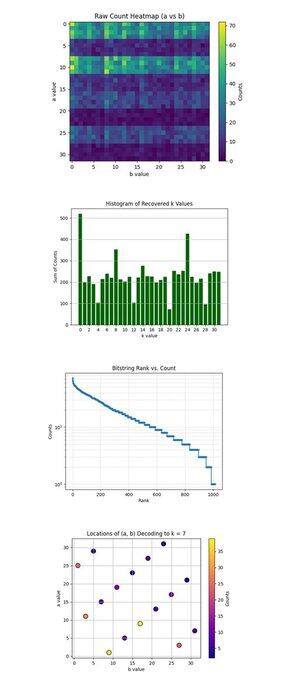Теплова карта необробленого лічильника (a проти b) вище (повний код на Qwork) показує, що сітка 32x32 представляє спостережувані кількості для кожної пари (a, b) після запуску схеми Шора. Теплова карта показує смугастий і нерівномірний розподіл, що вказує на перешкоди, а не на шум. Певні рядки (значення а) мають помітно вищу концентрацію, що свідчить про конструктивну інтерференцію уздовж конкретних рішень a + kb ≡ 0 mod 32. Гістограма відновлених k значень вище (повний код на Qwork) агрегує загальну кількість для кожного відновленого скалярного ключа k ∈ Z₃₂, отриману за допомогою k = −ab^(−1) mod 32. Домінуючими є величезний сплеск при k = 0 і ще один близько k = 24. Правильна клавіша k = 7 не є найвищою, але добре представлена (~54 + 41 + 32 = 127 відліків на кілька (a, b) пар). Це свідчить про те, що хакери можуть атакувати більшу кількість результатів. Наведений вище розділ Bitstring Rank vs Count (Log-Scale) (повний код на Qwork) показує Zipf-подібний графік рангу всіх бітових рядків за спадною кількістю. Вісь Y в логарифмічному масштабі показує експоненціальний хвіст, більшість результатів трапляються <10 разів. Бітові струни head (top ~50) мають значно вищу ймовірність, що вказує на піки конструктивних перешкод. Ви можете побудувати атаку квантового евристичного словника, яка збирає лише верхні N бітових рядків з експоненціальною віддачею сигналу. Це підтверджує, що квантова структура сигнал/шум все ще залишається незмінною навіть при довгих ланцюгах (глибина 67428). Розташування (a, b) Розшифровка до k = 7 вище (повний код на Qwork) показує, що кожна крапка є парою (a, b), яка декодується як k = 7. Інтенсивність кольору дорівнює кількості разів, коли ця пара зустрічалася. Графік показує відносно рівномірний розподіл по (a, b), але з локальними піками на (1, 9), (11, 3), (25, 1). Кратні (a, b) комбінації сходяться до k = 7 з нерівномірною кратністю. З криптоаналітичної точки зору, це підтверджує, що алгоритм Шора може надійно зламати ECC-ключі, навіть якщо правильне k не є результатом top 1. 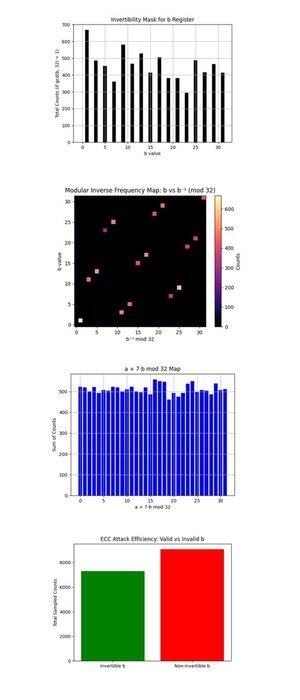Маска інвертовності для b Регістра вище (повний код на Qwork) показує гістограму лічильників для кожного b ∈ {0, ..., 31}, які співпрості з 32 (НСД(b, 32) = 1, тільки вони обернені за модулем 32 і корисні для відновлення k за допомогою: k = (−a)b^(−1) mod 32. Перевернуті «Б» добре населені, що свідчить про те, що схема дійсно дала кандидатів, яких можна відновити. Більша однорідність тут збільшила б потужність постобробки, в ідеалі вони були б плоскими. Модульна обернена частотна карта: b vs b^(−1) mod 32 вище (повний код на Qwork) показує теплову карту того, як часто кожна обернена b відображається на кожну відповідну модульну обернену b^(−1) mod 32, зважену за кількістю результатів. Більшість точок припадає на чисту бієктивну лінію, кожна b чисто відображає на унікальний b^(−1), підтверджуючи правильність модульної інверсії. Більш яскраві області (в нижньому лівому куті або вгорі праворуч) показують вибрані b з квантової вибірки. Немає позадіагонального шуму або скупчення, зберігається хороший знак чистої модульної структури. Карта a + 7b mod 32 вище (повний код на Qwork) припускає, що k = 7 і будує графік значення (a + 7b) mod 32 для всіх результатів. Розподіл майже рівномірний. Це говорить про відсутність різкого виступу перешкод, як у 4-бітному випадку. Чому? 5-бітна схема (з 10 логічними кубітами) розподіляє амплітуду тонше на 1024 результати, зменшуючи контрастність. Проте правильний ключ все ще можна було відновити, вказуючи на багато слабо конструктивних шляхів, а не на кілька домінуючих. Ефективність атаки ECC: Valid vs Invalid b вище (повний код на Qwork) показує загальну кількість зразків з інвертованим b (корисно для відновлення ключа) проти неінвертованим b (марно). Більше половини результатів витрачається на невірні значення b (НСД(b, 32) != 1). Наступний дизайн для 6-бітного розриву може використовувати маскування оракула або фільтрацію після вибору на допустимих b-доменах. 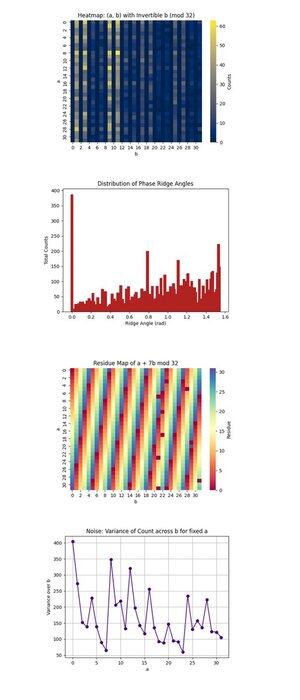Теплова карта: (a, b) з інвертованим b (mod 32) вище (повний код на Qwork) фокусується тільки на (a, b) парах, де b є оберненою модулем 32, необхідною умовою для відновлення k. Він показує, де концентрується квантова інтерференція в 1024-точковому просторі. Області високої інтенсивності виявляють бажані шляхи інтерференції, що свідчить про те, що квантовий стан еволюціонував нерівномірно, можливо, сприяючи певним орбітам при модульному множенні. Це підтверджує достатньо сильну злагодженість сигналів у деяких регіонах, щоб ізолювати дійсних кандидатів. Наведений вище розподіл кутів фазових гребенів (повний код на Qwork) об'єднує кути, утворені векторами (-a, b) на площині, за модулем π, які приблизно відповідають фазовим гребеням у просторі QFT. Піки на гістограмі вказують на сильні вирівнювання, резонанси, виду u + kv ≡ 0, що означає, що схема успішно закодувала k в інтерференційну картину, навіть якщо повний простір станів величезний. Множинні домінуючі кути свідчать про наявність гармонік прихованого зсуву. Карта залишків a + 7b mod 32 вище (повний код на Qwork) візуалізує вихідний залишок для конкретного цільового ключа k = 7, у всьому просторі (a, b). Будь-які узгоджені смуги або симетрії тут вказують, наскільки добре перешкоди посилюють допустимі рішення (де це значення дорівнює 0). Ви можете спостерігати, які області решітки 1024 відповідають a + 7b ≡ 0, підтверджуючи, що структура оракула призвела до успішного відбиття ключа. Шум: Дисперсія кількості через b для фіксованого a вище (повний код на Qwork) показує, наскільки шумними або стабільними були вихідні лічильники для кожного фіксованого a в міру того, як ми змінюємо b. Висока дисперсія означає, що деякі значення b призводять до сильного посилення, а інші ні, маючи на увазі чутливість схеми або внутрішній шум для цього a-рядка. Гладкі області означають квантову когерентність, тоді як шипи можуть вказувати на декогерентність або поширення помилок під час оцінки оракула. В результаті, цей експеримент успішно зламав 5-бітний ключ еліптичної кривої, використовуючи алгоритм Шора, виконаний на 133-кубітному квантовому процесорі IBM, розширивши попередній 4-бітний результат на значно більший інтерференційний простір (32x32 = 1024 результати). Ця схема кодувала оракул через Z₃₂ без жодного посилання на секретний скаляр k, і використовувала модульну групову арифметику, щоб заплутати скаляр у фазовій інтерференції. Квантова схема, глибиною понад 67 000 шарів, створювала дійсні інтерференційні картини, незважаючи на екстремальну глибину ланцюга, а класична постобробка показала k = 7 у топ-100 обернених (a, b) результатів. За допомогою візуалізацій цей експеримент підтвердив діагональні структури гребенів, маски інвертності та гармонійне вирівнювання інтерференційних гребенів, підтвердивши, що квантова когерентність залишається достатньо сильною, щоб посилити правильну модульну залежність. Це встановлює, що алгоритм Шора продовжує масштабуватися в більш глибоких режимах схем, і що стратегії відновлення ключів на основі словника (перерахування топ-100) залишаються життєздатними зі збільшенням довжини біта, демонструючи явну квантову перевагу навіть в шумних реальних умовах. Код # Головний ланцюг # Імпорт Імпорт журналів, JSON з математики імпорт НСД імпортувати numpy як np з qiskit імпортувати QuantumCircuit, QuantumRegister, ClassicalRegister, transpile з імпорту qiskit.circuit.library UnitaryGate, QFT з qiskit_ibm_runtime імпорту QiskitRuntimeService, SamplerV2 Імпорт панд як PD # IBMQ ТОКЕН = "YOUR_IBMQ_API_KEY" ЕКЗЕМПЛЯР = "YOUR_IBMQ_CRN" BACKEND = "ibm_torino" CAL_CSV = "/Користувачі/steventippeconnic/Завантаження/ibm_torino_calibrations_2025-06-26T02_21_07Z.csv" ПОСТРІЛІВ = 16384 # Параметри іграшкової-кривої (підгрупа порядку-32 з E(F_p)) НАКАЗ = 32 # |E(F_p)| = 32 P_IDX = 1 # Генератор P -> індекс 1 Q_IDX = 23 # Публічна точка Q = kP, тут "23 mod 32" для k = 7 # Помічник у веденні журналу logging.basicConfig(level=logging .INFO, format="%(asctime)s | %(назва_рівня)s | %(повідомлення)») log = logging.getLogger(__name__) # Вибір кубіта на основі калібрування def best_qubits(csv_path: str, n: int) -> list[int]: df = PD .read_csv(csv_path) df.columns = df.columns.str.strip() переможців = ( df.sort_values(["Помилка √x (sx)", "T1 (нас)", "T2 (нас)"], ascending=[Правда, Брехня, Брехня]) ["Qubit"].head(n).tolist() ) log .info("Найкращі фізичні кубіти: %s", переможці) Повернення переможців N_Q = 5 N_Q_TOTAL = N_Q * 3 # а, б, точка ФІЗИЧНИЙ = best_qubits(CAL_CSV, N_Q_TOTAL) # Constant-adder за модулем 32 як багаторазові ворота def add_const_mod32_gate(c: int) -> UnitaryGate: ""Повертає 5-кубітний вентиль, який відображає |x⟩ ↦ |x+c (mod 32)⟩."" mat = np.zeros((32, 32)) для x в діапазоні (32): мат[(x + c) % 32, x] = 1 return UnitaryGate(mat, label=f"+{c}") СУМАТОРИ = {c: add_const_mod32_gate(c) для c в діапазоні(1, 32)} def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, константа): ""Застосувати |x⟩ → |x+константа (mod 32)⟩ керується одним кубітом.""" qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg]) # Оракул U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (індексна арифметика mod 32) def ecdlp_oracle(QC, a_reg, b_reg, point_reg): Для i в діапазоні (N_Q): константа = (P_IDX * (1 << i)) % ПОРЯДКУ Якщо постійний: controlled_add(qc, a_reg[i], point_reg, постійний) Для i в діапазоні (N_Q): константа = (Q_IDX * (1 << i)) % ПОРЯДКУ, якщо постійна: controlled_add(qc, b_reg[i], point_reg, постійна) # Побудувати повну схему Шора def shor_ecdlp_circuit() -> QuantumCircuit: a = QuantumRegister(N_Q, "a") b = QuantumRegister(N_Q, "b") p = QuantumRegister(N_Q, "p") c = ClassicalRegister(N_Q * 2, "c") qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts") qc.h(a) qc.h(b) ecdlp_oracle(КК, А, Б, П) qc.barrier() qc.append(QFT(N_Q, do_swaps=False), a) qc.append(QFT(N_Q, do_swaps=False), b) qc.measure(a, c[:N_Q]) qc.measure(b, c[N_Q:]) return QC # Виконання IBM Виконання service = QiskitRuntimeService(channel="ibm_cloud", token=ТОКЕН, instance=ЕКЗЕМПЛЯР) backend = service.backend(БЕКЕНД) log .info("Сервер → %s", сервер .name) qc_raw = shor_ecdlp_circuit() trans = transpile(qc_raw, backend=сервер, initial_layout=ФІЗИЧНІ, optimization_level=3) log .info("Глибина ланцюга %d, кількість затворів %s", trans.depth(), trans.count_ops()) sampler = SamplerV2(mode=backend) job = sampler .run([trans], shots=SHOTS) результат = job.result() # Класична постобробка creg_name = trans.cregs[0].name counts_raw = результат[0].data.__getattribute__(creg_name).get_counts() def bits_to_int(bs): return int(bs[::-1], 2) counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v для k, v у counts_raw.items()} top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True) # Критерії успіху. Перевірте 100 верхніх обернених рядків для k = 7 top_invertibles = [] для (a_val, b_val), частота зверху: якщо gcd(b_val, ORDER) != 1: продовжити inv_b = pow(b_val, -1, НАКАЗ) k_candidate = (-a_val * inv_b) % ЗАМОВИТИ top_invertibles.append((((a_val, b_val), k_candidate, freq)) Якщо len(top_invertibles) == 100: Перерва # Перевірка на успішність і результати друку found_k7 = будь-який(k == 7 для (_, k, _) у top_invertibles) Якщо found_k7: print("\nУСПІХ — k = 7 знайдено в топ-100 результатів\n") ще: print("\nУВАГА — k = 7 НЕ знайдено в топ-100 результатів\n") print("Топ 100 обернених (a, b) пар та відновлене k:") Для (а, б), к, рахують у top_invertibles: тег = " <<<" якщо k == 7 інакше "" print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count}){tag}") # Збереження необроблених даних з = { "experiment": "ECDLP_32pts_Shors", "backend": сервер .name, "physical_qubits": ФІЗИЧНІ, "ПОСТРІЛИ": ПОСТРІЛИ, "рахує": counts_raw } JSON_PATH = "/Користувачі/steventippeconnic/Документи/QC/Shors_ECC_5_Bit_Key_0.json" з open(JSON_PATH, "w") як fp: json.dump(вихід, fp, відступ=4) log .info("Результати збережені → %s", JSON_PATH) # Кінець Повний код для всіх візуалізацій з використанням даних запуску на Qwork.