Trendaavat aiheet
#
Bonk Eco continues to show strength amid $USELESS rally
#
Pump.fun to raise $1B token sale, traders speculating on airdrop
#
Boop.Fun leading the way with a new launchpad on Solana.
Lattice-based ZK/SNARKs lack a rigorous prototyping stack.
lattirust aims to fills this gap.
It's a modular Rust framework for benchmarking argument systems over SIS and MLWE.
Think arkworks for lattices, without shortcuts.
Let's unpack this one.
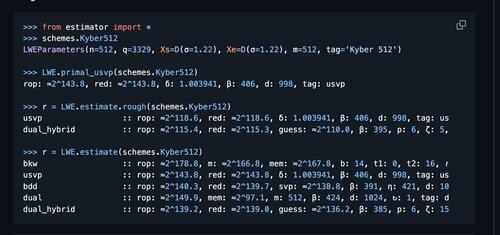
lattirust is a Rust library for prototyping and benchmarking lattice-based ZK/SNARK schemes. It occupies a niche similar to arkworks, but targets lattice primitives. Think of it as lattigo, but geared toward argument systems.
The library is modular, covering:
- lattirust-arithmetic: polynomial rings, linear algebra, challenge spaces
- lattice-estimator: concrete security estimation
- relations: abstractions for argument relations
- labrador, lova: implementations of recent schemes
Security estimation is currently based on lattice-estimator and PQ-Crystals. Future plans include a compile-time Rust-native estimator optimized for SIS assumptions, addressing the gap in tooling for argument-specific hardness.
labrador implements the LaBRADOR scheme, focused on lattice-friendly arguments.
lova adds folding-based techniques inspired by Lova ZK protocols, indicating ongoing exploration into succinctness and efficiency under lattice assumptions.
Future work includes parameterised polynomial arithmetic (supporting non-NTT or partial-NTT domains) and modulus-lifting for q ≡ 5 mod 8. The roadmap hints at deeper optimisation for arithmetic-heavy cryptographic contexts.
There's integration with nimue and partial compatibility with arkworks, suggesting an intention for broader ecosystem interoperability. Notably, Nethermind’s latticefold was built on an early fork of lattirust.
The team is actively working on ZK proofs for MLWE and RLWE encryption schemes (KLSS23, Libert24) and constant-time FHE ops in Jasmin, targeting high-assurance use cases with formal verification through hacspec, Jasmin, EasyCrypt, and Lean.
Overall, lattirust is positioning itself as a comprehensive base layer for high-assurance, lattice-based ZK systems. The tooling and architecture cater to experimental design and concrete instantiation of lattice-based proof systems.
Repo:
5,24K
Johtavat
Rankkaus
Suosikit













